2022. 11. 20. 16:12ㆍ데이터구조
이진탐색트리를 배우는 이유
이진탐색트리가 널리 활용되는이유?
-구조가 단순하다
-쉽게 노드의 키들의 정렬된 결과를 얻을 수 있다.
-이진 검색과 비슷한 방식으로 아주 빠르게 탐색 할 수 있다.
이진탐색트리(binary search tree)란?
이진탐색(binary search)의 개념을 트리 형태의 구조에 접목한 자료구조
이진탐색트리의 조건
각 노드 키가 왼쪽 서브트리에 있는 키들보다 크고, 오른쪽 서브트리에 있는 키들보다 작다.
일반적으로 키값이 같은 노드는 복수로 존재하지 않아야한다.

이진참색트리의 구조
노드의 왼쪽 서브트리에는 그 노드의 값보다 작은 값들을 지닌 노드들로 이루어져있다.
노드의 오른쪽 서브트리에는 그 노드의 값보다 큰 값들을 지닌 노드들로 이루어져있다.
루트의 왼쪽 서브트리와 오른쪽 서브트리는 이진탐색트리이다.
이진탐색트리에 사용되는 노드
key:키값을 저장(탐색에 사용)
value:값을 저장
left: 왼쪽자식 참조
right:오른쪽자식 참조

이진탐색트리 클래스
클래스이름: BinarySearchTree
생성자는 멤버변수 root 생성

이진탐색트리는 노드를 이용하여 구현된다.
삽입연산
이진탐색트리에 새로운 노드를 삽입
노드를 삽입한 뒤에 트리의 형태가 이진 검색 트리의 조건을 유지해야함
노드 삽입과정
1. 삽입위치찾기
삽입하는 키를 k라고 하자
k가 루트 키 보다 작으면 왼쪽서브트리에 삽입, k가 루트 키 보다 크면 오른쪽서브트리에 삽입
만약, k가 루트의 키와 같다면 루트의 value를 교체한다
이 과정을 서브트리에서 반복하여 삽입 위치를 정함
2. 새로운 노드를 삽입위치에 추가


재귀적 방법으로 노드를 삽입하는 방법
1.서브트리의 루트노드를 sroot라고 가정
2.sroot의 키 보다 삽입할 키가 작으면 sroot의 왼쪽 서브트리에 노드 삽입하는 재귀함수 호출
3.sroot의 키보다 삽입할 키가 크면 sroot의 오른쪽 서브트리에 노드 삽입하는 재귀함수 호출
삽입연산
insert():전체트리에 노드를 삽입
-파라미터:
-key: 삽입하는 노드의 키
value: 삽입하는 노드의 값
insert_to_subtree(): 서브트리에 노드를 삽입
-파라미터
-key:삽입하는 노드의 키
-value:삽입하는 노드의 값
-sroot: 서브트리의 루트 노드
리턴: 없음

탐색트리 클래스 생성
생성자 self.root 는 none = 빈트리
insert 메소드로 전체트리에 노드 삽입
루트노드 유무부터 탐색 if 문을 사용해 self.root: 루트노드가 있다면 self.insert_to_subtree 함수로 서브트리로 이동
루트노드가 없다면 else 로 self.root=Node(key,value) 노드를 생성한다
서브트리에 노드 삽입하는 메소드
if 로 키값이 서브트리의 루트노드의 키보다 작다면 if key< sroot.key: 에서 또 if 문을 사용해 왼쪽자식이 있을때와 없을떄로 나눈다. if sroot.left: <- 왼쪽 노드가 있으면 sroot의 왼쪽서브트리에 노드를 삽입한다. self.insert_to_subtree(key,value,sroot.left)
else: sroot.left=Node(key,value)왼쪽 노드가 없으면 else 로가 sroot의 왼쪽자식으로 노드를 삽입한다.
#노드를 생성할땐 키값과 벨류값만
key가 서브트리의 루트의 키보다 크면 if 문으로 똑같이 오른쪽 자식이 있는지 없는지에 따라서 나눈다.
if sroot.right: <- sroot의 오른쪽 자식이 있으면, insert 함수를 재귀적으로 불러와 sroot의 오른쪽 서브트리로 간다.
없으면 노드를 생성한다. sroot.right=Node(key,value)
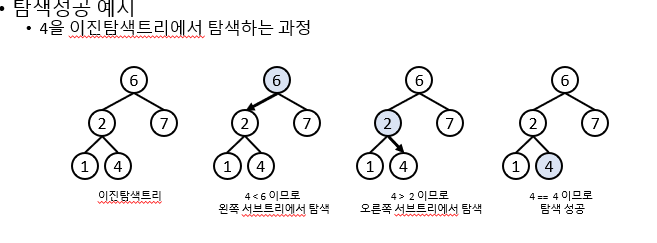
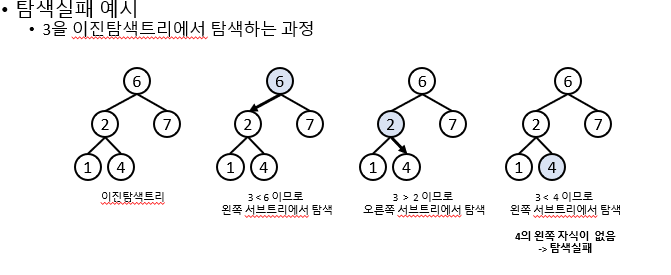
탐색연산
키값으로 노드를 탐색하는 함수
탐색알고리즘
탐색하는 키를 k라고 하자
k와 루트의 키를 비교
1.k==루트의 키: 탐색성공, 루트의 값을 리턴
2.k<루트의 키:왼쪽서브트리에서 k를 탐색
만약 왼쪽서브트리가 없다면 탐색 실패
3.k>루트의 키: 오른쪽서브트리에서 k를 탐색
만약 오른쪽 서브트리가 없다면 탐색 실패
노드 탐색 구현
탐색연산
find()
1.전체트리에서 노드를 탐색
2.성공시 노드의 값 리턴
3.실패시 None리턴
find_in_subtree()
1.서브트리에서 노드를 탐색
2.성공시 노드의 값 리턴
3.실패시 None 리턴

if not sroot:
return None -> 루트노드가 없으면 None을 리턴
elif key=sroot.key :
return sroot.value <-찾던 키와 서브트리의 키가 같으면 탐색 성공 이고 키값을 리턴
elif key <sroot.key :
return self.find_in_subtree(key,sroot.left) <- 찾던키가 루트노드보다 작을경우 재귀함수를 사용해 왼쪽 서브트리로 가서 다시 탐색
else :
return self.find_in_subtree(key,sroot.right) <-찾던키가 루트노드보다 클경우 재귀함수를 사용해 오른쪽 서브트리로 가 다시 탐색
최소키 탐색
-이진탐색트리에서 키값이 가장 작은 노드를 찾는 과정
루트의 왼쪽서브트리가 있다면 왼쪽서브트리에서 다시 탐색

최대키 탐색
-이진탐색트리에서 키값이 가장 큰 노드를 찾는 과정
루트의 오른쪽서브트리가 있다면 오른쪽 서브트리에서 다시 탐색

최소키/최대키 탐색 구현
min_node()
서브트리에서 최소키값을 가지는 노드 리턴
max_node()
서브트리에서 최대키값을 가지는 노드 리턴

서브트리에서 최소키값을 가지는 노드 리턴
if not sroot : # 루트노드가 없다면
return None -> 루트노드가 없으면 None 리턴
else:
if sroot.left:
return self.min_node(sroot.left) -> 왼쪽 자식 노드가 있을시 재귀함수로 그 자식의 왼쪽 서브트리로 다시 간다
else: return sroot -> 왼쪽 자식 노드 없을시 노드 리턴
서브트리에서 최대키값을 가지는 노드 리턴
if not sroot:
return None <- 루트가 없을경우 None 리턴
else: if sroot.right :
retrun self.max_node ( sroot.right) -> 오른쪽 자식노드 가 있을경우 재귀호출로 그 자식의 오른쪽 서브트리로 이동
else:
return sroot <-오른쪽 자식노드 없을경우 노드 리턴
'데이터구조' 카테고리의 다른 글
| 데이터구조-정렬 (0) | 2022.12.03 |
|---|---|
| 데이터구조-이진탐색트리 트리순회 (0) | 2022.11.26 |
| 데이터구조-이진탐색트리 노드 삭제 (0) | 2022.11.21 |
| 데이터구조-트리 실습문제 (0) | 2022.11.11 |
| 데이터구조 - 트리 (1) | 2022.11.10 |